A. Introduction

Situations in which flows occur between a rotating inner cylinder and a stationary outer cylinder are found widely in industry (e.g. in motor shafts, in vehicle transmissions, in oil drilling operations etc.). The presence of rotation may have a large effect on the flow and heat transfer. Flow effects are discussed in this present section and the associated heat transfer behavior is discussed in Section 183.

The flow between concentric cylinders with rotation of inner one can be considered a composition of three basic flows: Couette, Poiseuille and Taylor, which can be either laminar or turbulent. As illustrated in Figure 1, the Couette flow is caused by rotation of inner cylinder and the Poiseuille flow takes place due to pressure difference between channel inlet and outlet. Taylor flow appears due to centrifugal forces after a critical rotation condition is achieved and is characterized by a sequence of toroidal vortices, which are distributed tangentially and with alternate directions.

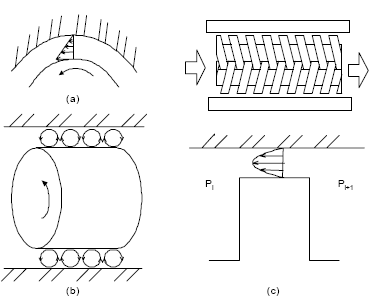
Figure 1 Schematic illustration of possible flow types inside of annular channels with rotation of the inner cylinder: a) Couette flow, b) Taylor flow and c) Poiseuille flow

Kaye and Elgar (1957) show experimentally that, depending on axial and tangential velocities, these basic flows will form four different regimes: laminar, laminar with Taylor vortices, turbulent and turbulent with Taylor vortices [see Figure 2(a)]. When the flow is laminar, the axial and tangential components of the fluid velocity are independent of each other. In this case, it is clear that rotation will not influence axial friction losses. On the other hand, when the Taylor vortices appear in the flow due to centrifugal forces — after a critical rotation — or when the flow is turbulent, these fluid velocity components are not independent anymore. Consequently, in these regimes the rotation of the inner cylinder is expected to influence axial friction losses. Actually, several authors confirmed the influence of rotation on friction factor. Yamada (1962), for instance, shows that there is an increase in the friction factor as rotation rate, which is represented by Taylor number, is increased. In Figure 2(b), horizontal lines represent friction factor values obtained with usual channel flow channel flow correlations. When the flow is laminar [Re_z = 1000, Figure 2(b)] there is a sudden increase at a certain critical tangential velocity. At this point — that corresponds to the appearance of Taylor vortices — the velocity components abruptly stop being independent of each other and the rotation of inner cylinder becomes important. For turbulent flow, velocity components are always dependent of each other and, therefore, the rotation influence is less important than in laminar case. The higher is the axial velocity the lower is the influence of the rotation.