After calculating the exit temperatures in the rating calculation, or having determined the flow length in the sizing calculation, the pressure losses may be calculated. The pressure loss for each stream through the heat exchanger finned passages is calculated by

\[\label{eq1} \Delta p=\frac{G^{2}_{c}}{2}\left[\frac{(K_{c}+1-\sigma^{2})}{\rho_{1}}+2\left(\frac{1}{\rho_{2}}-\frac{1}{\rho_{1}}\right)+\frac{f}{\rho_{m}}\frac{A}{A_{c}}-\frac{(1-\sigma^{2}-K_{e})}{\rho_{2}}\right] \tag{1}\]

where subscripts 1 and 2 denote the entering and leaving fluid density.

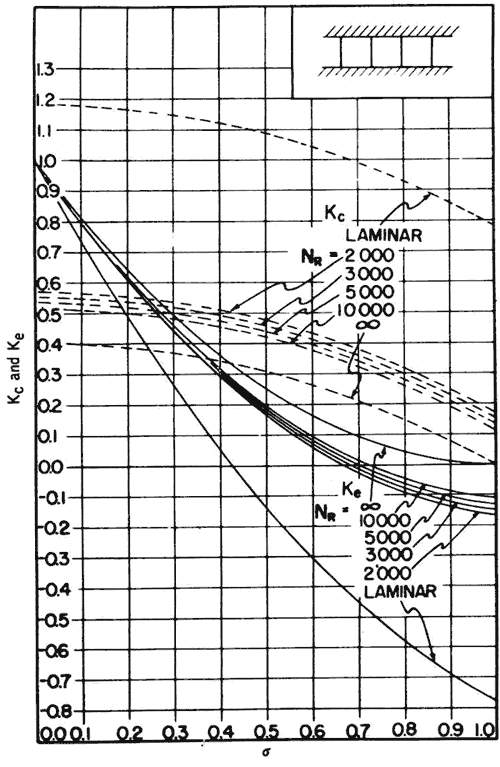
The terms of Equation 1 are entrance loss, flow acceleration loss, core friction, and exit loss, respectively. The K_c and K_e values depend on the cross-sectional flow geometry, σ and Re. Figure 1 gives K_c and K_e for a 1:1 ratio channel (Kays and London, 1984). Kays and London (1984) give similar curves for two other channel geometries (parallel-plate channel and triangular channel). The entrance and exit losses are normally < 10% of the total core loss, so the data of Figure 1 will cover most situations with adequate accuracy. The differences due to other channel configurations should cause only a second-order effect for most situations. Figure 1 is based on a uniform velocity entering the heat exchanger and fully developed flow in the core, and at the exit. This assumption is not valid for interrupted fin surfaces. In this case, Kays and London (1984) recommend the use of the Re = ∞ curves to evaluate K_c and K_e. In this case, all channel configurations have the same K_c and K_e values for Re = ∞. The calculation steps for the core pressure loss requires the information developed through step 6 of the rating calculation procedure. After calculation of the K_c and K_e values and the densities entering and leaving the core (ρ₁, ρ₂), the core Δp may be calculated using Equation 1.

Figure 1 Entrance and exit loss coefficients for multiple square channels with abrupt contraction entrance and abrupt expansion exit. Reynolds number is marked as N_R = Re, from Kays and London (1984)